As you probably know, for the past few months, a controversy has been raging about hydroxychloroquine. Some people think it’s effective to treat COVID-19, whereas others think it doesn’t work or even that it’s harmful. One might have thought that only experts would get emotionally involved in this debate, but amazingly it has become a huge political issue. In the US, Trump endorsed the treatment, which could explain why it became political, but it’s the same thing in France where this explanation isn’t available, so I think it rather speaks to the ability of the culture war to move even into seemingly technical, non-political issues. Anyway, I don’t really care about hydroxychloroquine (I know people don’t believe me when I say that, but it’s true), so I’m not going to argue either for or against it. Instead, I want to focus on a study that was published in the New England Journal of Medecine a few weeks ago, because I think it illustrates a widespread problem about how negative results are interpreted in both the scientific literature and the media, as well as the low quality of medical research.
The study in question is a randomized controlled trial of hydroxychloroquine used as post-exposure prophylaxis for COVID-19. (At least that’s what the authors claim, but one could argue they were at least in part testing whether hydroxychloroquine was effective as a treatment used early after infection, although I won’t be discussing this question.) They enrolled 821 people who were asymptomatic at the beginning of the trial, but had likely been exposed to people with COVID-19, either because someone in their household had been infected or because they were healthcare workers and were exposed to someone with COVID-19 at work. Participants were randomly assigned to either the treatment or control group and were shipped hydroxychloroquine or a placebo immediately afterward. Outcome data were collected online through a questionnaire filled by the participants themselves. After 14 days, 49 of 414 (11.8%) of the people in the treatment group were deemed to have COVID-19, whereas 58 of 407 (14.3%) of the people in the control group were, but the difference was not statistically significant.
This study was immediately hailed as proving that hydroxychloroquine was not effective against SARS-CoV-2 and, to this day, continues to be cited whenever someone claims that hydroxychloroquine works. Again, I’m not saying that hydroxychloroquine is effective against the virus whether as prophylaxis or treatment (I have no idea), but what I know is that it makes no sense to draw this conclusion from that study. People think it follows from the fact that, although the proportion of participants who ended up infected was smaller in the treatment group than in the control group, the difference wasn’t statistically significant. But despite a widespread misconception to the contrary, the fact that a study failed to find a statistically significant effect is not, in and of itself, evidence that there is no effect. In the case of this study, not only is the result not evidence that hydroxychloroquine is not effective, but to the extent that it’s evidence of anything, it’s evidence that hydroxychloroquine reduces the probability of infection.
Indeed, not only did less people end up infected in the treatment group than in the control group, but the study had very low power, so that it failed to find a statistically significant effect is exactly what one should have expected even if there was a pretty large effect. Statistical power was low because, when they did their power analysis to determine what sample size they would need, the authors assumed that hydroxychloroquine reduced the probability of infection by 50%, an implausibly large effect size. (I doubt that, even among the most vocal champions of hydroxychloroquine, there are many who think it’s that effective.) But as you assume smaller, and more realistic, effect sizes, power drops very rapidly. So the sample size of that study was insufficient to reliably detect a plausible, though still large, effect size of hydroxychloroquine on the risk of infection.
Moreover, power was further reduced by measurement error, since less than 20% of the people deemed positive for COVID-19 were tested by PCR. Indeed, the study was conducted in March in the US and Canada, when there was a shortage of tests. So the vast majority of symptomatic participants were diagnosed based on the symptoms they reported through the online questionnaire they were asked to fill out. Although the diagnosis was established by 4 infectious disease physicians, since the study took place in March, there must have been a lot of false positives, because there are many people with flu-like illnesses that can easily be confused with COVID-19 based on their symptoms around that time of year. Beside SARS-CoV-2, flu-like illnesses can be caused not only by influenza, but also by respiratory syncytial virus, rhinoviruses, etc. In fact, in the vast majority of cases, we have no idea what causes them. Even in France at the peak of the epidemic, where it was government policy to test only people with acute symptoms, the proportion of PCR tests that came back positive never exceeded 27%.
In addition to false positives, there must also have been false negatives, if only because some people who are infected with SARS-CoV-2 are either asymptomatic or mildly symptomatic. Now, you may think that preventing asymptomatic or mildly symptomatic infections is not really important, since by definition those people are not at risk of dying or suffering any kind of serious health issue, but they may still be able to infect other people who could die or develop a more serious form of the disease. Both false positives and false negatives constitute measurement error and, since the data was collected through a questionnaire that participants had to fill out online, it presumably wasn’t even the only source of measurement error. Now, it’s well-known that measurement error reduces statistical power, but amazingly the authors of the study don’t even mention that and apparently no referee asked them to address this issue.
I did a simulation to estimate the statistical power of this study, which takes into account measurement error due to the lack of PCR testing, but not that due to the fact that people no doubt made some mistakes when they filled out the questionnaire. For the purposes of this simulation, I have assumed that hydroxychloroquine reduced the risk of infection by 25%, which is smaller than what the authors of the study assumed in their power analysis but still pretty large, since in the long-run it could translate into dozens of thousands or perhaps even hundreds of thousands lives saved if the treatment were generalized. Moreover, I have assumed a base rate of infection of 15% among people who have been exposed to someone with COVID-19, which is higher than what the authors assumed in their power analysis but is approximately the proportion of participants who tested positive in the control group of the study. Thus, since I assumed that hydroxychloroquine reduced the risk of infection by 25%, it means the probability of infection in the treatment group was 11.25%.
I have also assumed that PCR testing has a sensitivity and specificity of 100%, which is of course false. I have also assumed that only 20% of people with symptoms were tested by PCR. Since less than 20% of people deemed positive were tested by PCR, this means that P(PCR | symptoms & non-infected) > P(PCR | symptoms & infected), even though it’s almost certainly the opposite. As for the symptoms-based diagnosis, I have assumed that it had a sensitivity of 91% and a specificity of 55%, based on the performance of a model trained on a sample of healthcare workers in the Netherlands discussed in this paper. Moreover, I have assumed that, 14 days after exposure, 30% of people who had been infected were still asymptomatic. Finally, I have assumed that, among people who had not been infected with SARS-CoV-2, 10% nevertheless developed symptoms because they had something else. Since I have assumed that 30% of people infected with SARS-CoV-2 were asymptomatic, this means that, if every participant had been tested by PCR and PCR testing were perfectly reliable, more than 50% of the people tested would have been positive for SARS-CoV-2, which as far as I know is higher than what has been observed anywhere in the world. To be sure, the participants of the study were known to have been exposed to someone with COVID-19, so you would arguably expect the rate of positive tests to be higher than average in this sample, but probably not that much higher.
With those assumptions, the simulation finds that statistical power was only ~15%, which is ridiculously low. I think the assumptions I made are pretty conservative, but if you disagree, I invite you to play with the simulation whose code I uploaded on GitHub and see for yourself what power it finds. I have tried many different combinations of assumptions and power was always extremely low. In fact, even when I assume that every participant is tested by PCR, power is only 23% with the effect size I have posited, so measurement error is not the main culprit. Even when I assume that hydroxychloroquine reduces the risk of infection by 50%, which is the assumption made by the authors in their power analysis, but otherwise make the same assumption as above, the simulation finds that power is only 55%, against 78% with no measurement error. By contrast, the authors were aiming for a statistical power of 90%, which is far more than the actual power because attrition was higher than they anticipated and, even more importantly, because they didn’t account for measurement error.
It should already be clear now why it makes no sense to conclude from this study that hydroxychloroquine probably doesn’t work. If statistical power of that study was only 15%, the fact that it didn’t find a statistically significant effect is entirely unsurprising. On the contrary, even if hydroxychloroquine reduces the risk of infection by 25%, it was by far the most likely outcome. But it’s even worse than that, because if you look at the mean observed effect in 10,000 runs of the simulation, you see that it’s almost the same as the effect actually observed in the study: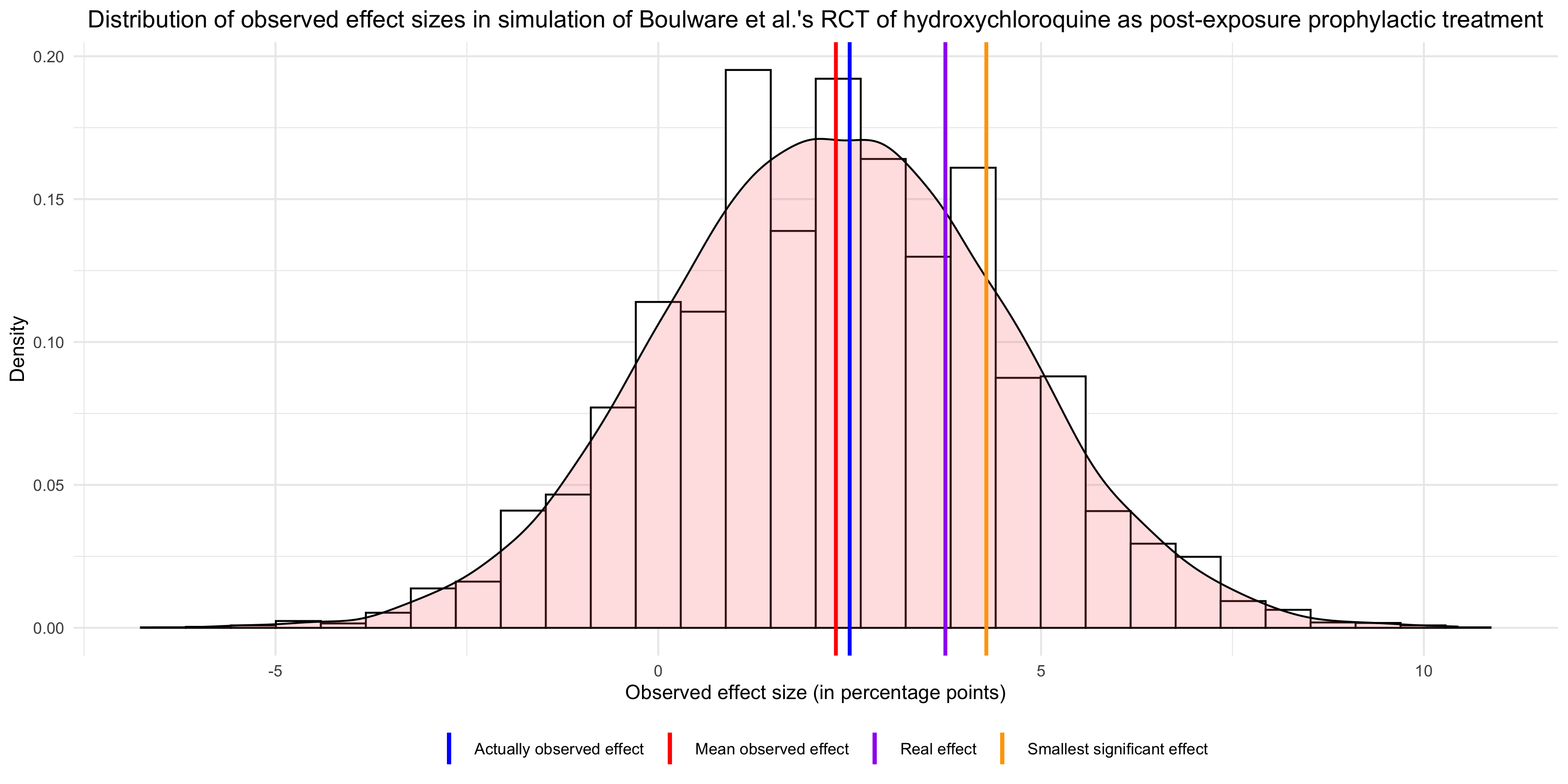
In other words, the results of that study are basically what you would expect if hydroxychloroquine had a modest prophylactic effect, so I don’t see why opponents of this treatment would feel vindicated by it. Sure, the effect was not significant, but that’s also exactly what you would have expected given that power was so low, so this can’t be evidence that hydroxychloroquine doesn’t work. Finally, the graph also shows that, had the observed effect been significant, it would have overestimated the real effect. This illustrates a well-known phenomenon, which Carlin and Gelman call a type M error, namely that observed effects that are statistically significant overestimate the real effect.
If you looked at the graph carefully, you may have noticed another interesting fact, namely that the mean observed effect is much lower than the real effect that I assumed for the purposes of the simulation. This is because, in addition to lowering statistical power, measurement error biased the estimate of the effect downward. The authors of the study, while acknowledging measurement error, seem to think it couldn’t bias the estimate:
Because of the lack of availability of diagnostic testing in the United States, the vast majority of the participants, including health care workers, were unable to access testing. Thus, an a priori symptomatic case definition was used — the U.S. clinical case definition of probable Covid-19. This trial represents real-world implementation after exposure. In the context of a randomized trial design, any non–SARS-CoV-2 viral infection (e.g., influenza, adenovirus, or rhinovirus) should be equally distributed in the trial groups.
They seem to be suggesting that, although there will be false positives due to non-SARS-CoV-2 infections, the rate of false positives will be the same in the control group as in the treatment group.
This is correct, but if hydroxychloroquine had a prophylactic effect, we’d expect less SARS-CoV-2 infections in the control group, hence proportionally more false positives. Thus, although false positives will artificially inflate the proportion of people who test positive for SARS-CoV-2 in both the treatment group and the control group, it will do so more in the former and will therefore bias the estimate of the difference between the groups downward. Similarly, even if the rate of false negatives is presumably the same in both groups, as long as hydroxychloroquine reduces the risk of infection by SARS-CoV-2, there will be proportionally more of them in the control group, because there will be more people who are infected with SARS-CoV-2. Thus, while false negatives will artificially deflate the number of people who test positive for SARS-CoV-2 in both the treatment group and the control group, it will do so more in the latter and this will further bias the estimate of the difference between the groups downward. (I’m not going to do it here because the formula is a mouthful, though it’s in the code I put on GitHub, but it’s easy to derive the expected observed effect with measurement error and show that it’s less than the real effect.) So measurement error didn’t just lower statistical power, it also biased the estimate downward, making the observed effect misleading, but the authors didn’t realize it.
To me, those problems seem pretty serious, since they make this study basically worthless. I sent a letter to the editor of the New England Journal of Medicine explaining them succinctly, but he chose not to publish it. Instead, he published a bunch of responses to the study, none of which addresses the points I made about measurement error. (One of them touched on the lack of statistical power, but did not connect it with measurement error, nor did it point out that measurement error biased the estimate of the effect downward. Still, in their reply to this letter, the authors of the original study totally failed to satisfactorily address the point about the lack of power, presumably because they can’t.) Of course, I’m a nobody, so perhaps my letter would have been published had I been a professor of medicine. But I’d say that it’s a pretty big problem if a nobody can spot mistakes in a study that was published in one of the most prestigious medical journals in the world. In fact, when I read the medical literature (which I have been doing more often lately), I’m often struck by how methodologically weak it is. I think researchers in that field should consider enlisting the help of statisticians to design their studies and analyze the results.
Again, I’m not saying that hydroxychloroquine works, either as prophylaxis or as a treatment for people who are already sick. In fact, if I had to guess, I’d say that it either doesn’t work or has a small effect. However, this is not because I have done a careful review of the literature (which I have not), it’s just because the vast majority of drugs that make it to the clinical stage development are never approved and, even when they do, effect sizes tend to be rather modest. Perhaps if I had read every study on hydroxychloroquine, I would have a different expectation, but I have not and, since I don’t care enough about this issue to do it, I’m just going to wait for the results of good quality studies. (Unfortunately, when it comes to hydroxychloroquine, it’s as if people on both sides of the debate conspired to only publish worthless crap. Again, I haven’t done a careful review of the literature, but every time a study is hailed by one side as providing definitive results, I read it and find that it’s terrible.) However, the people who study hydroxychloroquine and medical researchers in general are hardly alone in misinterpreting non-significant results, so I think it’s worth explaining why their interpretation is mistaken. People have talked a lot about p-hacking recently, but perhaps not enough about this, even though it’s a common problem. It’s probably not as bad as p-hacking, but it’s still problematic, especially since I think politically incorrect effects are prone to be declared non-existent based on underpowered studies.
Thanks.
Craps, as usual.
Why author of this article.. Not changing his conclusion… He should conclude Hcqs showed tendency to get some benefit in post exposure prophylaxis if started early.. Needs further randomised control trial with much larger study participants..