Lockdowns, science and voodoo magic

As Europe and the United States are experiencing a second or third wave of the pandemic, depending on how you count, the debate about lockdowns is raging again. Many people are convinced they are the best way to deal with the pandemic until a vaccine arrives. Back in the Spring, I argued in favor of lockdowns because we didn’t know much about the virus and Western governments were caught by surprise (I’m not even sure I was right anymore, even when you don’t look at things in retrospect with the information we now have, but that’s a question for another day), but now I think we should not resort to them anymore. The main reason is that, after looking at the data we have accumulated in the past few months, I have come to believe that lockdowns weren’t as effective as most people think relative to less stringent restrictions. People seem to believe that lockdowns are the only kind of policy that can prevent a colossal loss of life, because less stringent restrictions just don’t cut transmission enough. They also say a lot of things about lockdowns, especially about their effects on the economy, which I think are false, but in this post I want to focus on the claim that only lockdowns are really effective to cut transmission and ultimately prevent a lot of people from dying.

Whenever someone makes that claim, you can be certain they will cite the paper Flaxman et al. published in Nature a few months ago, which concluded that non-pharmaceutical interventions had saved more than 3 millions lives in Europe in the Spring and that among those interventions only lockdowns had a substantial effect. This paper went viral when it was published and continues to be cited all the time as proof that lockdowns saved countless lives during the first wave. This isn’t just true in informal discussions, but also in the scientific literature, where this paper is systematically cited to support the claim that lockdowns are very effective. (It’s already been cited almost 450 times since it was published a few months ago.) I hadn’t read it until very recently, but since the debate about lockdown has been rekindled by the second wave in Europe, I decided to read it and I was astonished by how bad it was. Since it still plays a very important role in that debate, I think it’s important to explain why it’s bad, so in this post I’m going to take it apart and explain why even Flaxman et al.’s own analysis shows that, while lockdowns do make a difference, they don’t cut transmission that much more than other, less stringent and therefore less costly restrictions. (I basically taught myself Stan over a weekend to do this, so someone should probably check my code, though I’m pretty sure there are no major mistakes.) After pointing out that it changes the policy debate quite a lot, I conclude with a few remarks about the role bad science has played in this debate and how this paper illustrates why the cult of science that many people have fallen into is bad.

What Flaxman et al. did

I’ve seen many people claim that Flaxman et al.’s paper showed that lockdowns were very effective, but I don’t think many of them know what they actually did in that paper, because it showed no such thing despite what the authors claim. In fact, what they did is assume that non-pharmaceutical interventions work (as we shall see, the model was bound to find that lockdowns specifically did most of the work, but more on that later), fit the data on deaths to a model that makes this assumption in order to infer various epidemiological variables of interest such as and the number of infections. Once this was done, they just compared the number of deaths predicted by this model, which by construction is going to be very close to the actual number of deaths, to the number of deaths in a counterfactual where there were no interventions. I will come back to this counterfactual, but first I want to say more about what this model, because it will be important to understand why this paper doesn’t show what Flaxman et al. claim it shows.

Here is the equation they use to model the true number of infections:It’s basically a discrete version of the SIR model, the most basic model of epidemiology. Don’t worry if mathematical symbols scare you, what it says is just that, on any given day, the number of people who get infected depends on the number of people who got infected previously and are still infectious, when they were infected, as well as on the reproduction number , which is the average number of people that a person who is infected goes on to infect.

Lockdowns and other non-pharmaceutical interventions affect the number of infections through their effect on . Here is how they model the way in which those interventions affect :Again, it’s not a big deal if you don’t understand everything, what you need to remember is that each non-pharmaceutical intervention is assumed to affect immediately, only non-pharmaceutical interventions are supposed to affect it and each is assumed to have the same effect in every country where it’s implemented.

Many people have criticized the first assumption, but while it’s no doubt unrealistic, the second and third assumptions seem even worse. Indeed, it’s obvious that even in the absence of any government interventions, people would still change their behavior in response to the pandemic because they’re afraid. This would reduce transmission and therefore it’s not true that only non-pharmaceutical interventions affect . Moreover, there is also no doubt that each non-pharmaceutical intervention is not equally effective in every country where it’s implemented, so it’s not true that each intervention has the same effect in every country. First, although various restrictions are modeled as the same in the paper, they were actually pretty different. For instance, the intervention that Flaxman et al. call “public events banned” consisted in forbidding gatherings of more than 5 people in Austria, 100 people in France, 500 people in Sweden and 1,000 people in Germany, but in the model all those different policies are treated as identical. Indeed, even “lockdown” was not the same thing everywhere, since under “lockdown” people in France couldn’t leave their place without filling a form while in Denmark people could meet as long as they were no more than 10.

Not only very different interventions are treated as the same in the model, but even if they had really been identical, their effect in different countries would still have been different for idiosyncratic reasons. Everybody has noted how people in some cultures might be more willing to follow rules, but there are many other possible factors that could also affect how effective the same intervention would be in different countries, such as differences in the proportion of people who need to take public transportation to go to work, differences in the age distribution of the population, etc. As you can see above, Flaxman et al. did include a country-specific effect in the model, which is supposed to model the fact that, precisely for this kind of idiosyncratic reasons, we don’t expect that even the same non-pharmaceutical interventions will be equally effective in every country. I will come back to this country-specific effect later, because it plays a very important and largely unacknowledged role in Flaxman et al.’s paper, but for the moment it’s enough to say that it’s only associated with the last intervention, which is a lockdown in every country except in Sweden where it’s the ban of public events. So the model only acknowledges that idiosyncratic factors could affect how effective the same interventions are in different countries for lockdowns but not for the other interventions.

Another problem with the model is that it assumes the population of each country is homogenous, which is undoubtedly false and might result in getting the dynamic of the epidemic wrong even in the early phase, though as I have discussed before we don’t really know. (Some people seem to think that, since I wrote this, various things have shown that the naive model was correct, but they are confused. However, there is only so much you can talk about in one post, so perhaps I will revisit that issue some other time.) I just mention that issue because I think it’s important and people should try to model heterogeneity more often, if only as a robustness check, but I won’t be focusing on that in the rest of this post because we don’t know how much it matters and, even if heterogeneity actually had a large effect on the dynamic of the epidemic and the final attack rate, I think not modeling it would mostly affect their counterfactual and not their estimates of the effect of non-pharmaceutical interventions.

Finally, they don’t fit their model on data about cases, but instead assume a particular infection fatality rate for each country and use this plus the infection-to-death distribution to work backward from data on deaths and infer the number of infections over time. (The infection fatality rates they use are derived from Verity et al.’s paper and adjusted for each country based on age-specific mixing patterns.) To be more specific, they assume that the reported daily number of deaths in a country follows a negative binomial distribution with mean , which they modeled like this:Again, don’t worry if you don’t understand everything, what’s important is just that you understand that Flaxman et al. assume a particular infection fatality rate and a distribution of the delay between infection and death (both of which are estimated from data collected early in the pandemic), which they use to infer the daily number of infections during the period they consider by working backward from the data on deaths. This is a good idea because, while data on deaths are hardly perfect, there are definitely more reliable than data on cases, which are a mess.

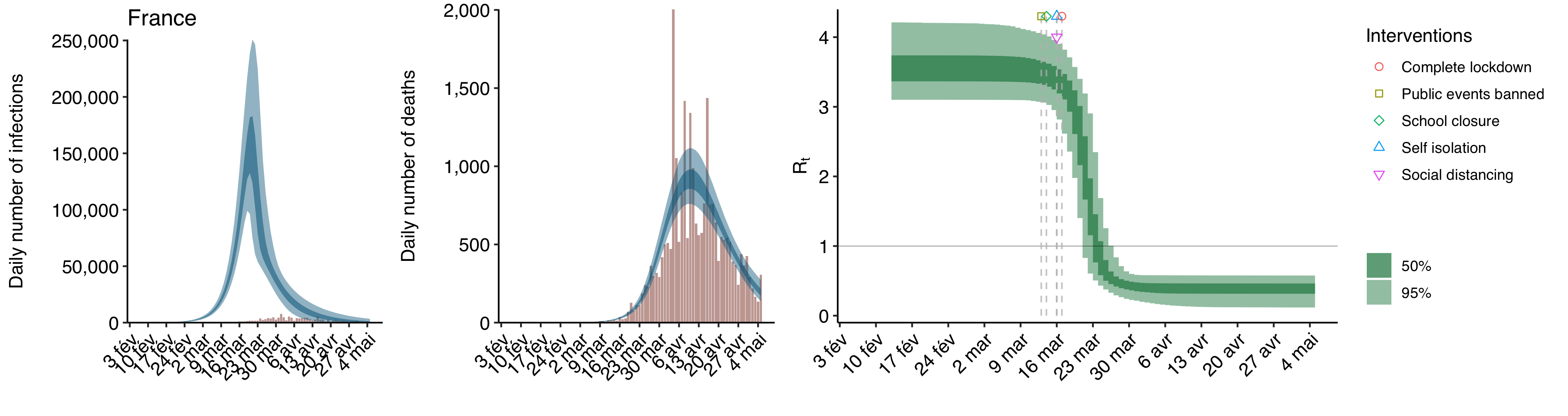
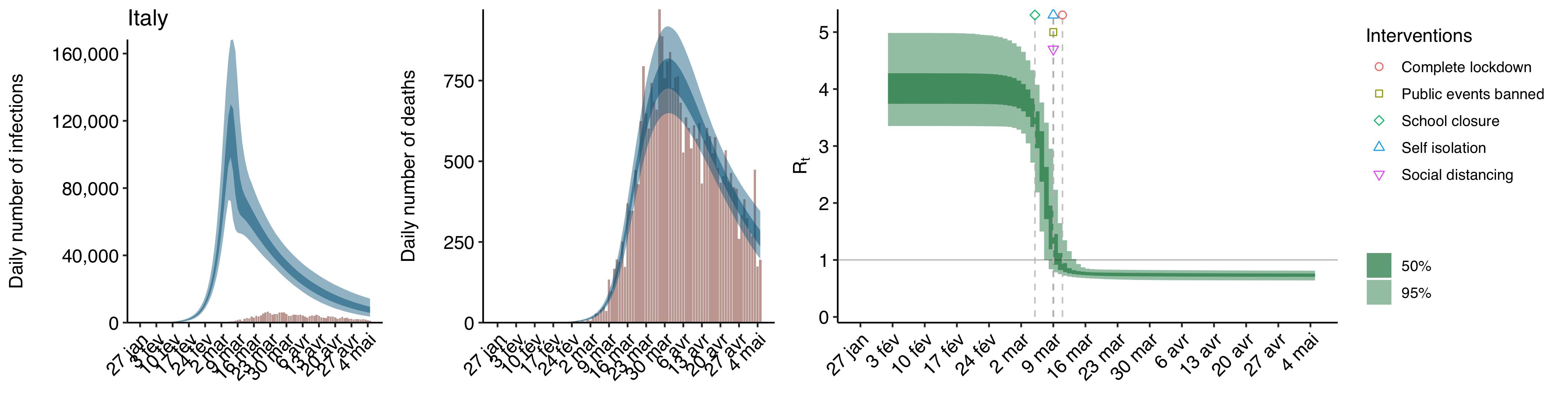
Anyway, I’ll go back to the model they used later, but you know enough about it for now, so let’s talk about their results. Here is a replication of what is arguably the most important chart Flaxman et al. put in their paper, which shows the effect of each intervention on :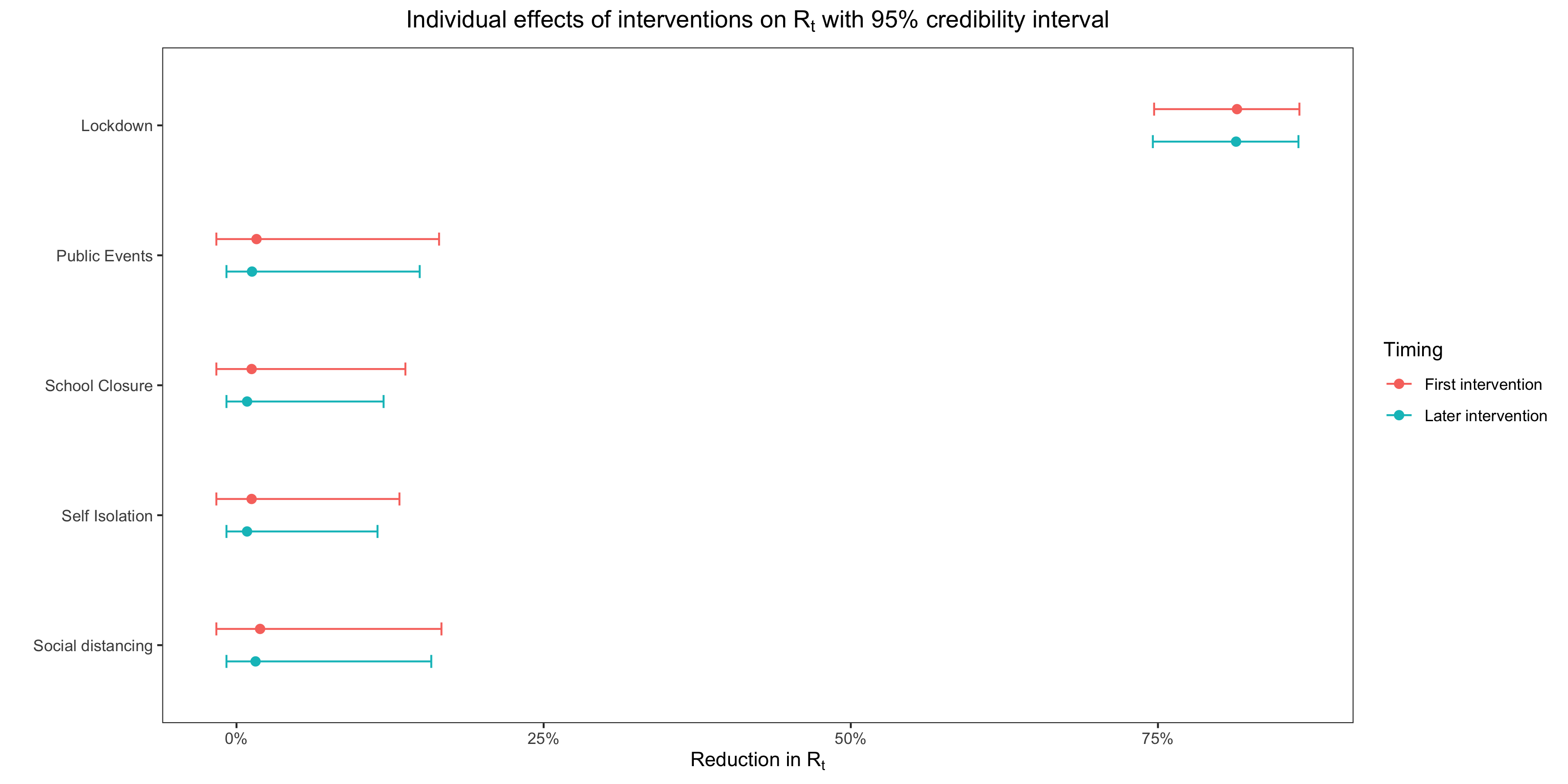As you can see, according to their model, only lockdowns had any effect on the reproduction number, while the other interventions had no meaningful effect.

That’s the first headline, i. e. lockdowns have a huge effect on transmission and nothing else does, but what about the other, i. e. non-pharmaceutical interventions saved more than 3 million lives in Europe during the first wave? Here is the table in their paper that shows how many lives, according to their model, were saved by non-pharmaceutical interventions during the first wave for each country: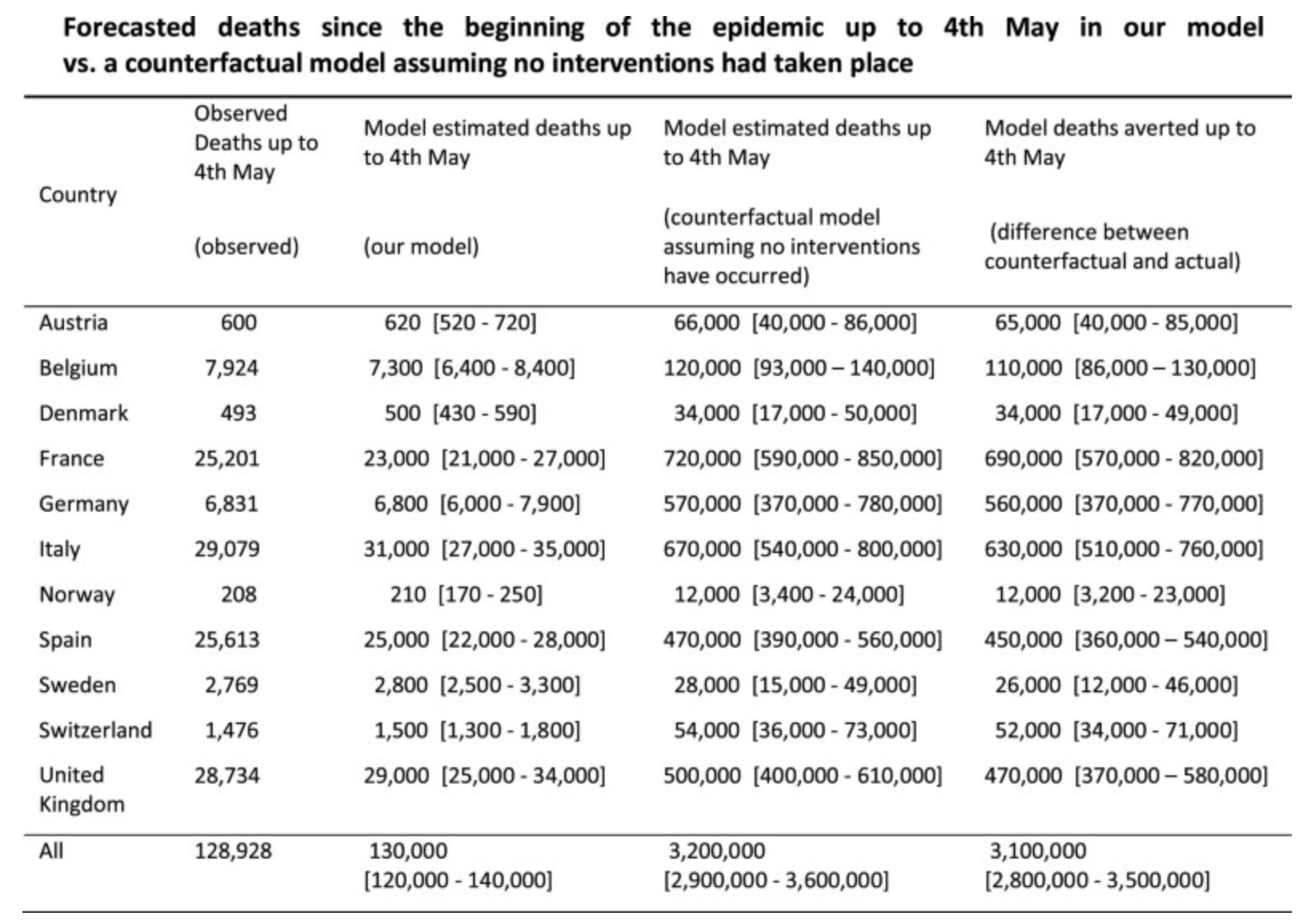Since as we have seen, they also found that, except for lockdowns, no interventions had any meaningful effect on transmission, it follows that lockdowns are responsible for the vast majority of the more than 3 million lives saved.

In order to reach this estimate, they had to estimate the number of deaths the pandemic would have caused in a counterfactual where there were no interventions, since the number of deaths averted by restrictions is just the difference between the actual number of deaths and the number of deaths there would have been in that counterfactual. What they did to estimate how many people would have died in the absence of interventions is just take the estimates of they obtained for each country by fitting their model with interventions and run the same model without interventions starting from that basic reproduction number. As many have noted, this is completely unrealistic, because even in the absence of interventions by the government, people would still have changed their behavior out of fear as they would have seen hospitals being overwhelmed and this would have reduced . To be sure, there would have been a lot more deaths, especially since there is a delay between infection and death, the process is near-exponential and people don’t really get scared and change their behavior until enough people have died, but it would still have resulted in significantly less than 3 million deaths. However, while this is the problem most critics of Flaxman et al.’s paper have focused on, it’s not the main problem with that paper.

Taking a closer look at the results

When I saw the table above, I immediately noticed that something didn’t make sense. As you can see in this table, the number of deaths that were averted by non-pharmaceutical interventions in Sweden according to the model is comparable to the number of deaths they averted in other countries, which suggests that Sweden’s policies to contain the epidemic were about as effective as the interventions in other countries. This is confirmed by plotting the overall effect of interventions in each country according to the model: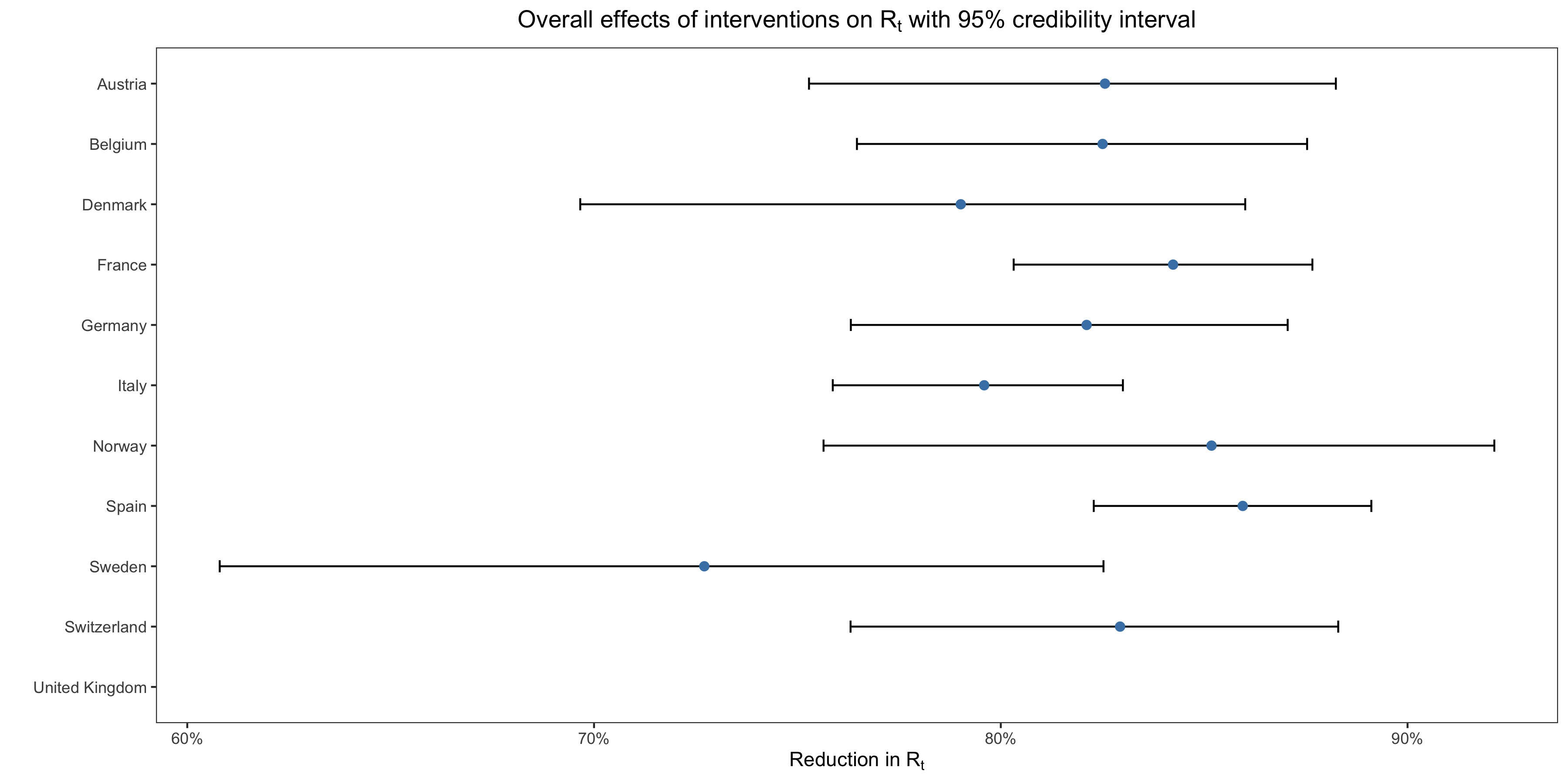However, still according to the model, only lockdowns had a meaningful effect on transmission and Sweden didn’t have a lockdown, so this doesn’t make sense.

The only way I could think to explain this anomaly is that, for Sweden but not the other countries, the country-specific effect in the model was huge. However, as far as can tell, Flaxman et al. don’t say what the country-specific effect was for Sweden either in the paper or in the supplementary materials. This immediately triggered my bullshit detector, so I went and downloaded the code of their paper to take a closer look at the results and, lo and behold, my suspicion was confirmed. In this chart, I have plotted the country-specific effect of the last intervention in each country: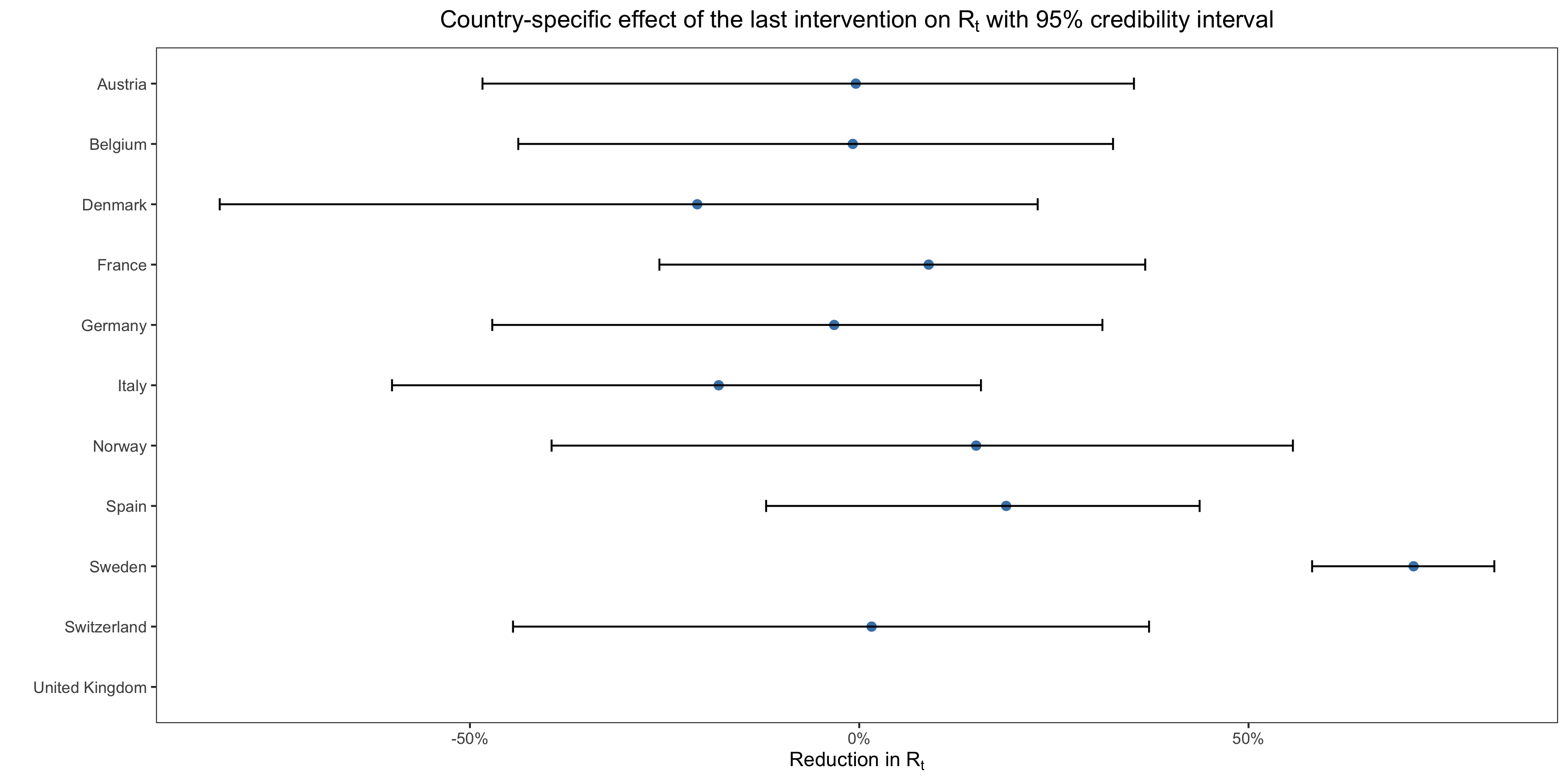As you can see, the country-specific effect for Sweden is gigantic, barely less than what the model estimates for the effect of a complete lockdown, whereas it hovers around zero for the other countries. Indeed, according to their prior on the country-specific effect, there was only a 1 in 4,000 chance that it would be that large. Moreover, the estimate is pretty tightly estimated for Sweden, but the credible intervals are extremely wide for the other countries.

Now, this completely undermines the conclusion Flaxman et al. draw from their results, so I understand why they swept that fact under the rug and didn’t show this chart anywhere in the paper or even in the supplementary materials… (What I don’t understand, or would not understand if I didn’t know how peer review actually works, is that no reviewer asked for it.) Indeed, the country-specific effect is supposed to model how the same interventions may not be equally effective in every country for idiosyncratic reasons, but unless you believe there is some kind of magic floating in the air in Sweden, it doesn’t make sense to believe that, for some mysterious reasons, banning public events was several orders of magnitude more effective over there than in the rest of Europe, despite the fact that it only banned events with more than 500 people and was therefore less stringent than in any other country except Germany. The obvious explanation is that the model is misspecified and that in fact it’s not the case that lockdowns did most of the work in reducing transmission. Instead, most of the heavy lifting was or would have been done by other, less stringent interventions plus more or less spontaneous behavioral changes. You don’t need a complicated model to reach this conclusion, you just have to look at the death curve in Sweden during the first wave or at the epidemic curve in other countries where there was no lockdown or where it wasn’t nearly as strict as in the Spring but where nevertheless fell below 1 to see that complete lockdowns aren’t necessary to break the epidemic, as Flaxman et al. claim based on results that obviously show no such thing.

I actually think that not mentioning this fact about the country-specific effect in Sweden comes very close to scientific malpractice. It makes their main conclusion, which as  just noted can be seen to be implausible without any complicated modeling, very hard to maintain and I have a hard time believing they weren’t aware of that and that it’s not why they carefully avoided the topic in describing their results. In any case, what is clear is that, once you realize that the model was only able to find that no intervention except lockdowns had a meaningful effect on transmission by estimating a huge country-specific effect for Sweden, it becomes impossible to take that conclusion seriously. As we have seen, the assumption that only non-pharmaceutical interventions affect is baked into the model, but prima facie it doesn’t assume that only lockdowns specifically have a significant effect on transmission. Flaxman et al. would probably say that it reached that conclusion from the data, but I think it’s largely artificial and that in practice the model was bound to find that only lockdowns had a large effect on transmission, even if they did not.

Why the model found that lockdowns single-handedly broke the epidemic

First, as Nicholas Lewis noted, their choice of prior for the effect of the interventions made the model far more likely to find that all but one or two interventions had almost no effect on . However, this is not the same as assuming that only lockdowns work, since this is compatible with another intervention being responsible for most of the effect on transmission. Again, Flaxman et al. would probably claim that, while their choice of prior made it more likely that the model would find that only one or two interventions had a meaningful effect on transmission, it reached the conclusion that only lockdowns had a meaningful effect from the data. However, I think that, insofar as it’s true, it doesn’t warrant the causal inference they make.

The first way to see this is to run the model separately on each country’s data instead of pooling as they did in the paper and look at the results for Sweden where there was no lockdown. As Flaxman et al. explain in the supplementary materials, where they show the results of this analysis for Sweden and 3 other countries, they actually tried that. As far as I can tell, they didn’t give the code for this analysis, but I was able to replicate it by adapting their code for the original, pooled model and here are the results for Sweden: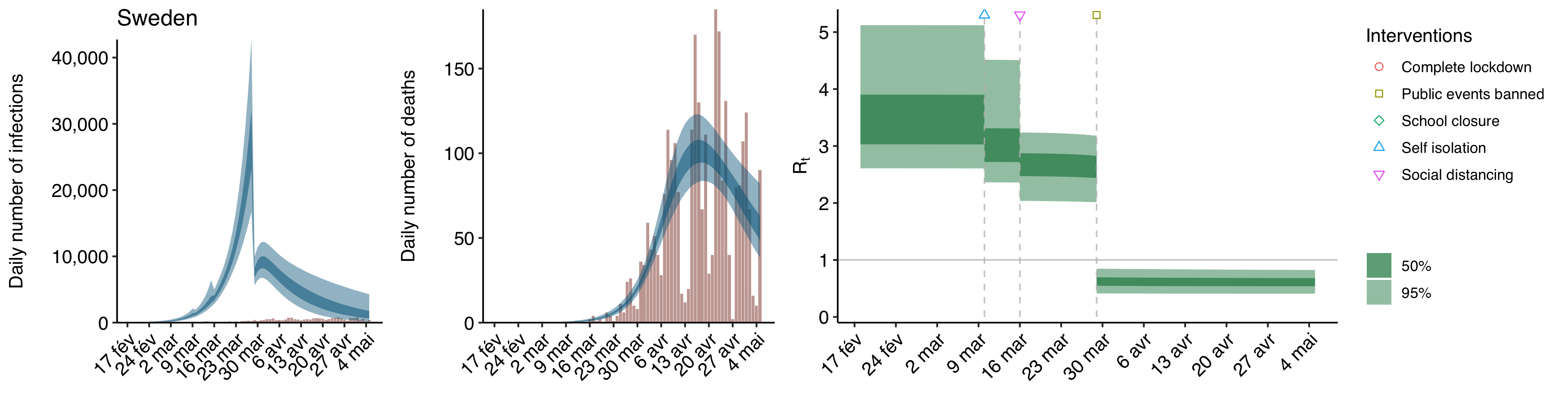As you can see, although the last intervention isn’t a lockdown, the model still finds that it had a huge effect on while the other interventions didn’t make a meaningful difference. Given what I noted about the country-specific effect in the version of the model that pools data from different countries to estimate the effect of interventions, this is entirely unsurprising, but although they show this chart in the supplementary materials, Flaxman et al. don’t point out that it totally undermines their conclusion.

Instead, it seems they just performed this analysis to argue that pooling was justified (see supplementary discussion 8 in the supplementary materials and their response to reviewer 3), on the ground that it allows to estimate the effect of each intervention more precisely since the model can use more data that way and that running the model separately on each country doesn’t meaningfully affect their conclusions anyway. I don’t find this argument very convincing, because if you have good reasons to think that a pooled model would be seriously misspecified, which is definitely the case here, then in my opinion the fact that pooling allows you to have more data to estimate the effects of interventions precisely and be less dependent on each country’s data reporting idiosyncrasies is not really a good reason to do it since the results are not interpretable. Again, if only because non-pharmaceutical interventions actually took very different forms in different countries even when they were treated as identical in Flaxman et al.’s model, we’d expect their effects to be pretty heterogenous across countries.

Moreover, the claim that pooling didn’t significantly alter the results — Flaxman et al. say they show “considerable agreement” with the non-pooled model — seems highly disputable, since when you plot the effects it looks like this in most countries: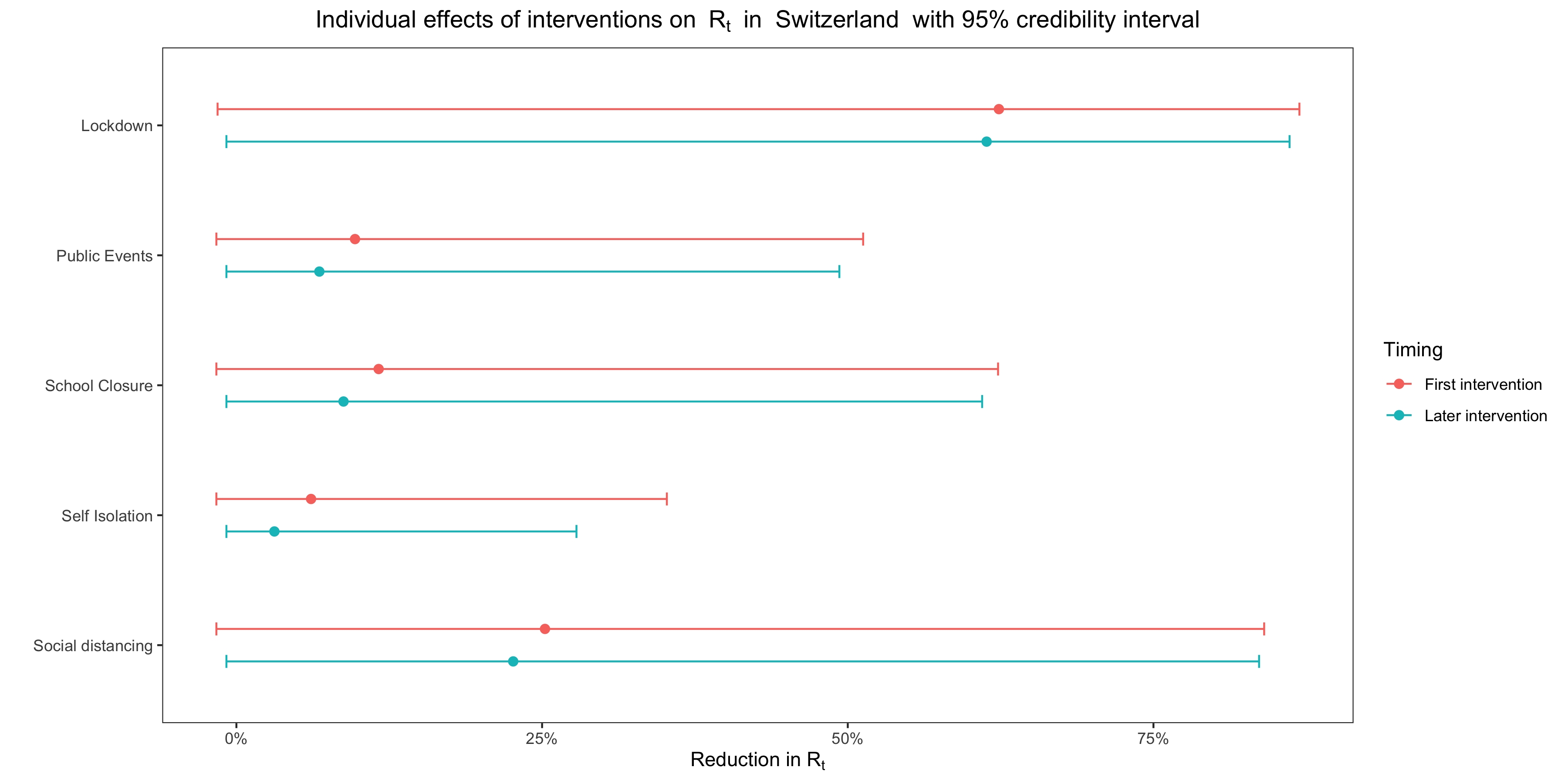This is not really surprising given that, in many countries, several interventions were implemented on the same day, but except in Belgium the credible intervals show considerable overlap with the effect of lockdown even in countries where that is not the case. Flaxman et al. interpret the more clear-cut results of the pooled model as a sign that it’s less sensitive to data reporting idiosyncrasies, but if you ask me it’s just as likely that it doesn’t mean anything.

But the most important point is that, as I just noted, the fact that in Sweden the model ascribed such a large effect to banning public events should have changed their conclusions, because it was a hint that, if their model ascribed the overwhelming majority of the effect on transmission to lockdown, it wasn’t because lockdown had been single-handedly responsible for breaking the epidemic but rather because, given the data on deaths and the timing of interventions, the model was bound to reach that conclusion even though it’s false. In order to verify this, I generated epidemic data with a simulation that assumes went down smoothly and that interventions had no effect on it whatsoever, which I then used to fit the model used by Flaxman et al. Here is a chart that shows the epidemic I simulated: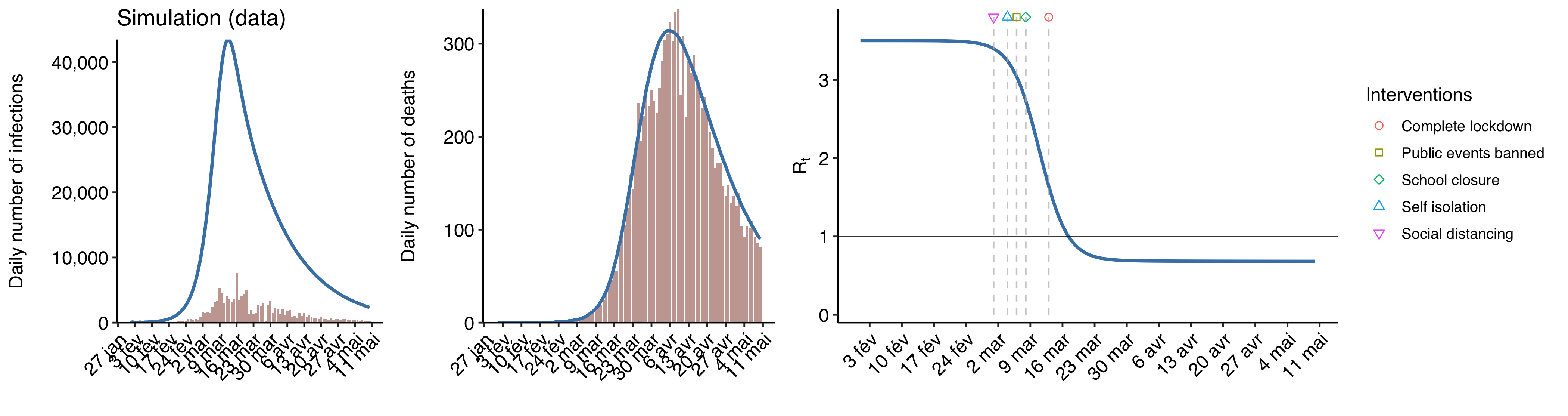The blue curve shows the actual epidemic, while the bars show data on reported cases and deaths. I assumed that had the form of a logistic function that starts from a of 3.5 and smoothly went down to 0.7 in about a month and just stayed at this level afterward. I generated the data on reported cases and deaths by assuming that only 10% of infections and 90% of deaths were detected and adding some noise to make them more like the sort of data we have about real epidemics.

I fit the model on the data about reported deaths and tell it that various interventions took place around the time that started to fall. (Of course, the model doesn’t know when started to fall, I just gave it the data on reported deaths and told it when each intervention was implemented.) In this case, we know that interventions had no effect whatsoever, since they played no role in the data generating process. In fact, I could have placed them anywhere I want, it wouldn’t have changed anything to the data on reported deaths I fed into the model. I told the model that the last intervention was a lockdown, but since it had no effect on , it shouldn’t find that it had a huge one while the other interventions had no meaningful effect unless it just ascribes a huge effect to whatever the last intervention happens to be, at least with that sort of data. But here is what the model inferred from the data I simulated about the dynamic of the epidemic: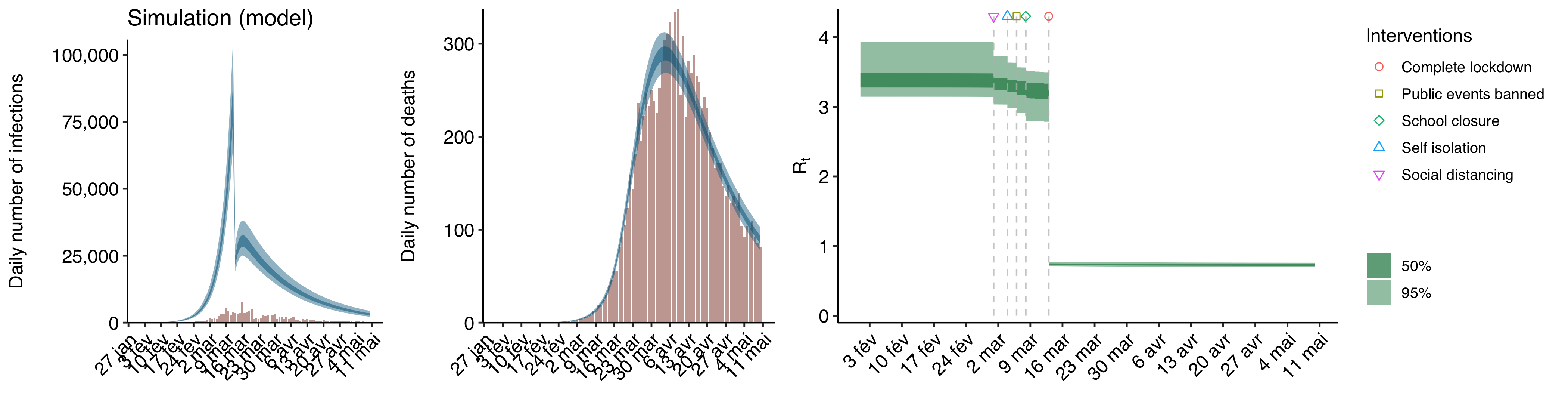The blue line curve shows the epidemic as inferred by the model, while the bars show the observed data it used to infer the epidemic. As you can see, it looks exactly like the results of Flaxman et al.’s analysis of real epidemic data, with a sudden fall of immediately after the lockdown is implemented. Again, if I had told the model that the last intervention was e. g. self-isolation, it would have found that self-isolation was single-handedly responsible for pushing below 1 instead.

Based on what I have seen by playing a bit more with simulations, it seems that the model tends to ascribe most of the reduction in to whatever intervention took place after the peak of infections and was closest to that peak or, if no intervention took place after the peak, to the last intervention. This makes sense when you think about it. Indeed, if you assume that one intervention is responsible for the overwhelming majority of the reduction in , the peak of the infections curve you infer is going to be located at the time this intervention took place. So both the infections curve and the deaths curve you infer are going to be shifted to the left or to the right depending on whether you assume that collapsed sooner or later. Moreover, since both the infection curve and the distribution of the delay between infection and death are right-skewed, the death curve, on which the model is fit, is also going to be right-skewed. Now, when a curve is right-skewed, the fit is going to be worse if the peak of infections, hence also the peak of deaths, inferred by the model is to the left of the actual peak than if it’s to the right. So the model is better off ascribing most of the reduction in to the intervention that happened closest to the peak of infections but after it, unless that intervention happened really too late after the peak.

It seems that it’s those purely mathematical considerations and the fact that lockdowns were implemented last and before or not too late after the peak of infections in every country, not the fact that lockdowns really are the only intervention that have a meaningful effect on transmission, which explain why the model reached that conclusion. (Of course, the lockdown probably had something to do with the fact that the peak occurred when it did, but my point is that it probably would have occurred around the same time even without lockdown and the model would have ascribed a huge effect to the previous intervention, as in Sweden.) Indeed, if this were not true, it’s extremely unlikely that it would also have found that banning public events, the last intervention in Sweden, had a very similar effect on as lockdowns in other countries. Flaxman et al. used their model to tell a wild causal story about what happened in Europe during the first wave, but as we have seen when I showed what happens when you fit the model on simulated data, the same model would also fit data generated by a completely different process than assumed by the causal story in question. Moreover, since Sweden was evidently able to push below 1 without a lockdown but with much less stringent interventions that can’t plausibly be assumed to have resulted in a sudden fall in transmission, was probably closer to what I assumed for my simulation than to the stepwise function estimated by Flaxman et al.’s model.

We don’t know enough to make causal inferences from the data

I have shown that Flaxman et al.’s model would also fit simulated data that were generated by a completely different process than it assumes, but can a model that assumes this kind of process also fit the actual data? Yes. Here is what happens when I fit on France’s actual data a model that, instead of assuming that is a stepwise function, assumes it has the form where is the growth rate of the logistic function that is subtracted from , is the sigmoid’s midpoint and is the final value of :As you can see, the fit is very good. I didn’t even bother computing any goodness-of-fit statistics, because I did this very quickly just to show that it could be done and I have no doubt that I could improve the fit by tweaking the model, but it’s clear just visually that it’s about as good as the fit of Flaxman et al.’s non-pooled model and perhaps even better.

Now, this model doesn’t make any assumptions about the effect of interventions, it just estimates the values of , , and that produce the best fit with the observed data on deaths. So it’s compatible with the hypothesis that lockdowns had a very large effect on transmission and, if you look at the it estimates when you fit it on France’s actual data, that’s definitely a story you could tell since starts falling very rapidly shortly after the lockdown came into effect. However, when you look at other countries such as Italy, the fit is no longer consistent with that story:As you can see, by the time the lockdown came into effect, was already near its final level according to the model. Thus, if you are committed to that model, you have to reject Flaxman et al.’s conclusion that only lockdowns were able to push below 1.

Of course, I’m not saying that you should be committed to this model, since there is no reason to believe that actually had this exact shape, although it’s probably a better approximation of the actual shape than a stepwise function. Moreover, as I already noted, this model doesn’t even try to estimate the effect of non-pharmaceutical interventions. However, I don’t see that as a problem, since I think it’s impossible to infer the effect of non-pharmaceutical interventions from the data on deaths and the timing of interventions anyway. Indeed, what this whole discussion shows is that we’re faced with a classic example of what philosophers of science call the underdetermination of theory by the data, i. e. the fact that you can always explain the same data by positing very different unobservable processes. In this case, the same data on deaths can be explained by completely different stories about how changed during the course of the first wave of the pandemic in Europe, because those stories imply a deaths curve that fit the data very well. Again, this is always the case, it’s not specific to lockdowns or epidemiology.

Some philosophers of science actually think that the underdetermination of theory by the data implies that we are never justified in believing that scientific theories, which explain phenomena by positing all sorts of unobservable entities and processes, are true. But most people still think that, despite the underdetermination of theory, we can sometimes figure out the causal structure of the world. The reason is that, although there are always many different theories that can explain the data, we often have background knowledge that we can use to rule out most of them. (It usually doesn’t rule out all of them, so in order to decide between the remaining theories, we have to make judgments about their relative explanatory power, a concept that philosophers of science also have discussed at length.) In the case of the pandemic of COVID-19, however, I don’t think we have enough background knowledge to estimate the effect of non-pharmaceutical interventions with the kind of data Flaxman et al. used.

In general, in order for statistics to be useful to learn something about the data generating process, you have to already know enough about the data generating process, because statistical techniques always rely on assumptions about the data generating process and are likely to mislead you if those assumptions are false. But I don’t think we know enough about how non-pharmaceutical interventions affect transmission to come up with a model that, knowing only how many deaths were recorded on each day and when each intervention came into effect, we can trust to estimate accurately the effect of each intervention on . Nor do we know enough about how people’s behavioral changes affect transmission and how people’s behavior would have changed in the absence of any non-pharmaceutical intervention to estimate how many lives non-pharmaceutical interventions have saved.

As we have seen enough, we know enough to say that Flaxman et al.’s model is unrealistic in several ways even before we have used it to estimate the effect of non-pharmaceutical interventions, but it’s hard to know before looking at the data how much it matters. However, as I have argued above, once you fit the model on the data and see what the results look like for Sweden, it becomes clear that it’s actually very misleading and that we shouldn’t take seriously the main conclusion Flaxman et al. draw from their results. This would have been clear if they had not swept under the rug the fact that the model estimated a huge country-specific effect for Sweden, but we didn’t need a complicated mathematical model to reach that conclusion, we just had to take a look at the deaths curve for Sweden and notice that, although there was no lockdown and the country only resorted to mild forms of the other interventions, was still pushed below 1. What Flaxman et al. did was use complicated statistical methods to reach a conclusion that was obviously false.

Using another counterfactual to estimate how many lives were saved by lockdowns

As we have seen, in order to estimate how many lives non-pharmaceutical interventions have saved in Europe during the first wave, Flaxman et al. used a counterfactual in which not only are there no such interventions but people’s behavior doesn’t even change, so the only thing reducing transmission is immunity building up in the population. (Even in this scenario, their model is probably not reliable because it assumes homogenous population mixing, but this is not important.) This counterfactual is not very interesting because virtually nobody is recommending that governments do nothing to contain the epidemic. The debate is about what kind of interventions should be used to do so. One reason people disagree about that is that they disagree about the benefits of different types of interventions. (Another reason is that they disagree about the costs of different types of interventions. There is a lot to be said on that issue, but this post is already long, so I will leave that for another time.) In particular, people disagree about how much lockdowns reduce transmission and how many lives they can save, so a more interesting counterfactual is a scenario in which there was no lockdown but European governments nevertheless took more limited steps to contain the epidemic with less stringent restrictions.

Since Flaxman et al. concluded that lockdowns were single-handedly responsible for almost the entirety of the reduction in , they would probably regard this counterfactual as for all practical purposes identical to the one they used in their paper, but as we have seen their conclusion is totally implausible, so in fact it’s a very different counterfactual. Unfortunately, if their conclusion can’t be taken seriously, it’s because their model is misspecified, so we can’t really use it to estimate that counterfactual by taking their estimate of the effect of each intervention and simulating a scenario in which lockdowns never happened but everything was otherwise the same. But we can use a workaround that, while not very rigorous, is still more informative than Flaxman et al.’s totally useless counterfactual. Since we can’t trust their estimates of the effect of individual non-pharmaceutical interventions, let’s just take their estimate of the overall effect in Sweden and use it to simulate a counterfactual in which every country reduced transmission by as much as Sweden did without a lockdown. More precisely, I assume that starts at the value of estimated by Flaxman et al.’s for each country and stays there until the moment when their lockdown came into effect, at which point it’s reduced by exactly as much as the overall effect of interventions in Sweden according to Flaxman et al.’s model.

Here is a table that compares how many lives are saved in each country if we use Flaxman et al.’s counterfactual to how many lives are saved if we use this counterfactual when the pooled version of the model is used: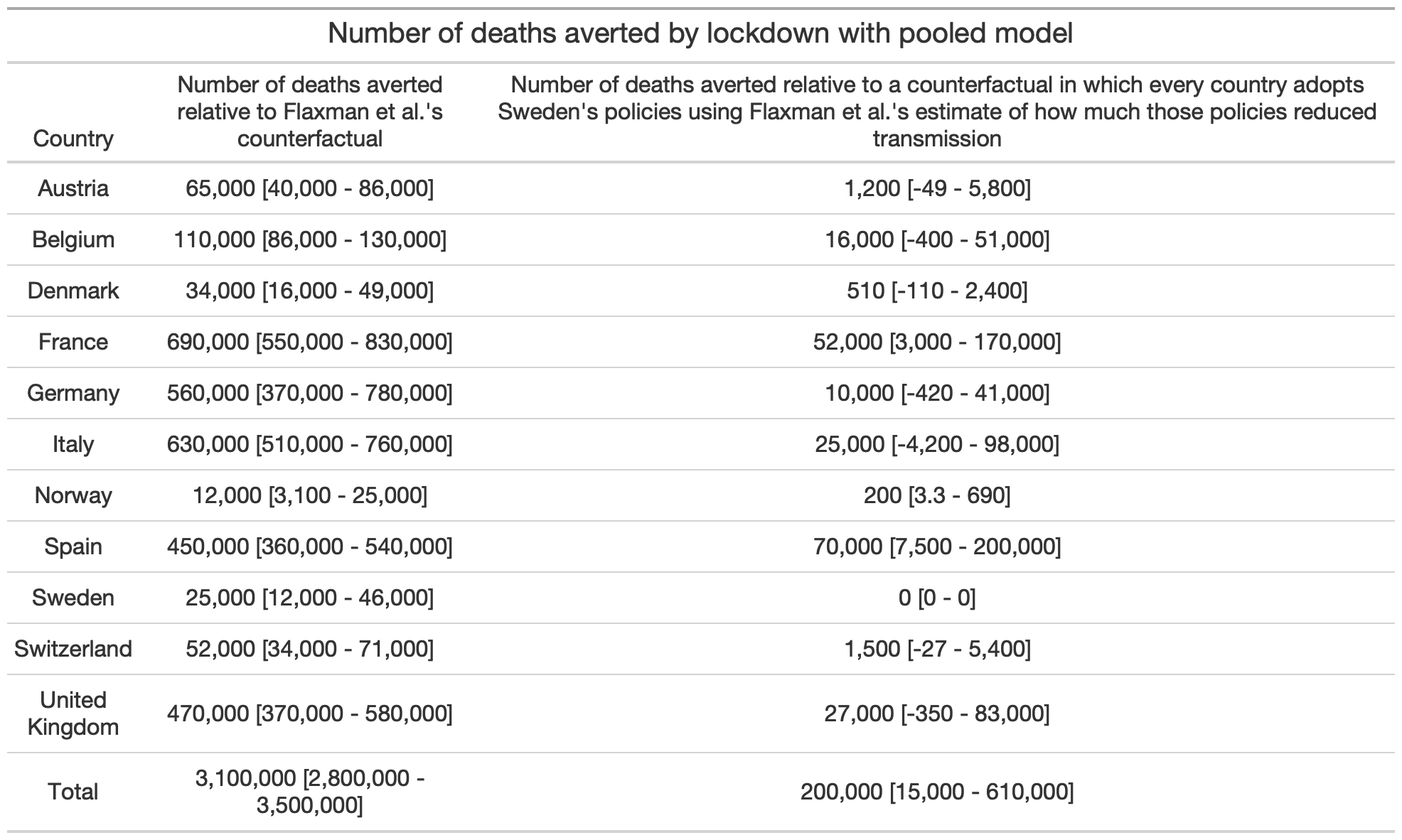As you can see, relative to Flaxman et al.’s counterfactual, the number of lives saved is divided by ~15.

Here is another table that shows the same thing but when the non-pooled version of Flaxman et al.’s model is used: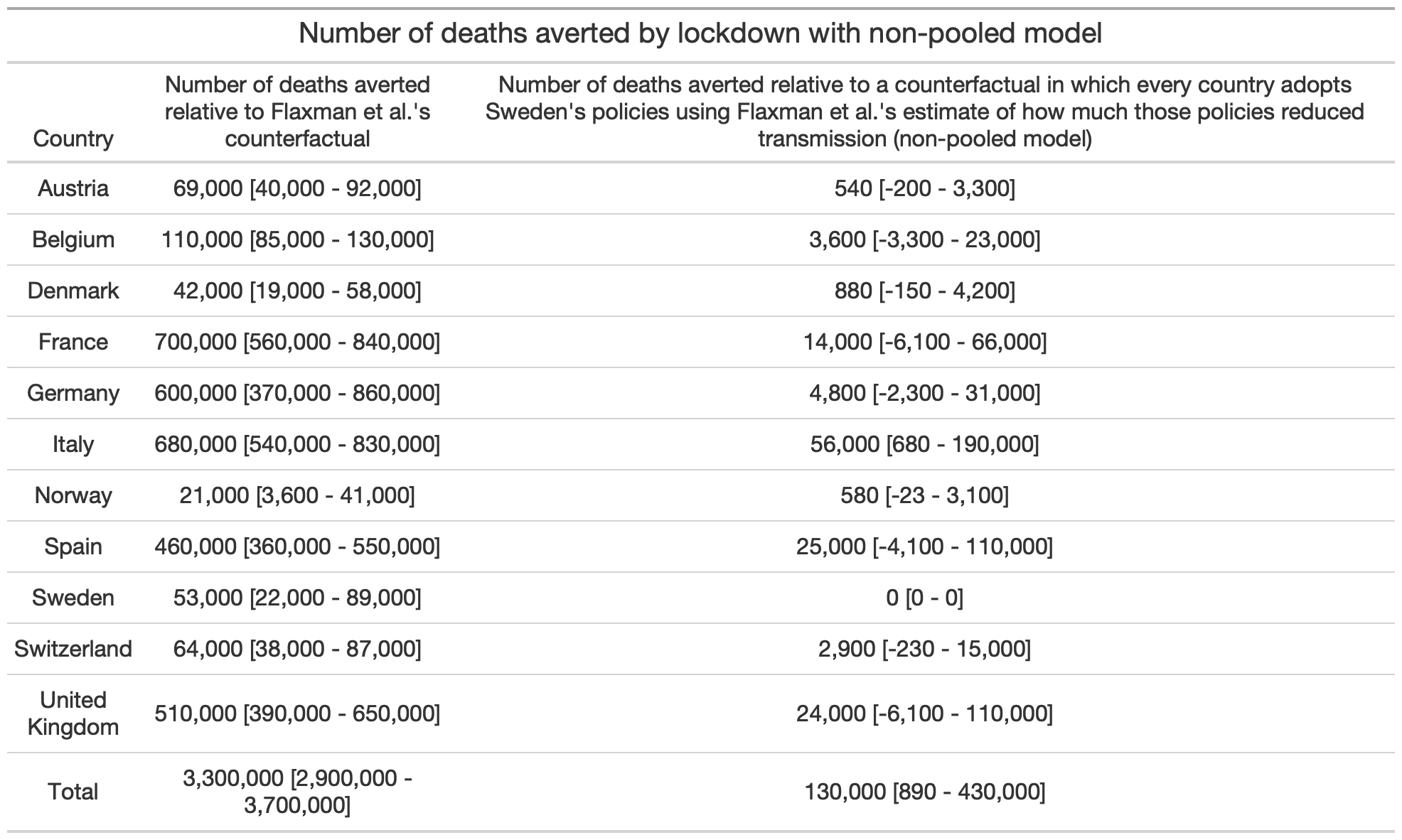With this version of the model, compared to Flaxman et al.’s counterfactual, the number of lives saved is divided by ~23.

To be clear, since they are based on Flaxman et al.’s estimate of the overall effect of non-pharmaceutical interventions in Sweden and their model is clearly misspecified, I don’t think we should take very seriously either of these estimates, though we should definitely take them more seriously than Flaxman et al.’s preposterous estimate. What really matters is that my counterfactual is based on Flaxman et al.’s estimate of how much interventions reduced transmission in Sweden, where there was no lockdown, which goes to show how ridiculous it was for them to conclude that only lockdowns have a meaningful effect on transmission. Again, if they were able to defend that conclusion anyway, it’s because they swept under the rug the fact that their model found a huge country-specific effect for Sweden’s ban of public events. (In the non-pooled model, the effect of the ban itself is comparable to the effect of a lockdown in the rest of Europe.) If they had made that clear, they couldn’t have defended this conclusion, because nobody would have bought that, for some mysterious reasons, banning public events had a several orders of magnitude larger effect in Sweden than anywhere else in Europe.

I actually think their model probably overestimated in most countries, so I suspect that lockdowns actually saved even less lives than what my estimates suggest, but the truth is that we don’t know and we have no way to know. What I think we can say with a great deal of confidence, however, is that lockdowns didn’t save anywhere near 3 million lives. (EDIT: Some people have asked me why I think that we can say that with a great deal of confidence. The answer is that we can because, in order to conclude that non-pharmaceutical interventions had saved 3 millions lives in Europe alone during the first wave, Flaxman et al. rely on a counterfactual in which more than 95% of the population had been infected by May 4 in every country, which is preposterous.) This matters because, if you think that lockdowns really saved 3 million lives, then they are a no-brainer from a cost-benefit perspective. But once you realize that, although we can’t say exactly how many lives they saved, it was much less than 3 million, it’s not so clear anymore. In fact, I think that, from a cost-benefit perspective, there is a very strong case against lockdowns and in favor of using much less stringent restrictions to contain the epidemic. I was planning to discuss that at length, but this post is already long, so I think it’s better to wait until I write something more focused on that issue, because people have been making a lot of incredibly confused arguments in the cost-benefit debate and I really think a thorough refutation is necessary.

Speaking of confused arguments, many people claim that, since Sweden’s neighbors only had a fraction of the deaths it did, most of the deaths in Sweden could have been prevented with a lockdown. Of course, you would reach a completely different conclusion if you compared Sweden to some other countries, such as Spain, that recorded more deaths per capita despite having a lockdown. But people argue that we should only compare Sweden to its neighbors, because they have a similar culture, so they provide the best counterfactual. However, this argument is totally unconvincing, because in any country the epidemic is affected by countless factors and we don’t have a very good idea of what most of them are. Culture is probably one of them, but it’s not the only one and almost certainly not the main one. We also don’t know exactly what aspects of culture matter. It could be that, although overall Sweden is culturally closer to other Nordic countries, it’s actually closer to other European countries with respect to the cultural factors that matter the most for the pandemic. So we are in no position to claim that other Nordic countries provide the best comparison. This is a very basic and obviously correct methodological point, I don’t think it would be remotely controversial if Sweden had not become such a fixation in the debate about the best policy response to the pandemic, but unfortunately it has and that’s why I see people who teach causal inference professionally make this argument all the time.

Again, I don’t think we should take very seriously the estimates of the number of deaths averted by lockdowns I obtain with my alternative counterfactual, but I still think that looking at the estimates for Denmark and Norway in the table I showed above should give pause to people who find the argument that we should only compare Sweden to its neighbors convincing. Indeed, according to this table, Denmark and Norway barely saved any lives by implementing lockdowns rather than using only the same, less stringent restrictions as Sweden. (Although it’s worth noting that, compared to lockdowns in countries such as Spain, Italy or France, the lockdowns in Nordic countries were pretty lax, so the difference with Sweden was never as big as most people imagined anyway.) The precise estimates I obtained don’t mean a lot, because they are based on Flaxman et al.’s model which as I have argued is misspecified, but they nevertheless suggest that even if Denmark and Norway had only been able to reduce transmission as much as Sweden, they would still have significantly fewer deaths per capita. I think what mattered the most for the eventual death toll, beside perhaps how much “dry tinder” there was in Sweden compared to its neighbors, is the timing of the interventions relative to that of the epidemic.

All European countries implemented their interventions around the same time, but for whatever reasons (which had nothing to do with policy), the epidemic just happened to be more advanced in some countries than others by the time this happened and as a result more people died over there. If more people died in Sweden than in other Nordic countries, it’s not just because there was more “dry tinder” and the government adopted a more relaxed policy in Sweden, but probably also because other countries were lucky that, by the time interventions were implemented and people started to change their behavior as they realized the danger, the epidemic was still at a relatively early stage. But even if you think that all the COVID-19 deaths that occurred in Sweden during the first wave could have been prevented if the government had ordered a lockdown, which is preposterous, what this would mean is that ~5,000 mostly very old people were allowed to die so that 10 million others could live a much more normal life than anywhere else in Europe. Perhaps you think it wasn’t worth it, but if you think that’s obvious, then I’m sorry but you are delusional.

To some extent, European countries have learned that complete lockdowns were unnecessary to contain the epidemic and didn’t pass a cost-benefit test, since they have implemented much less stringent lockdowns than what they did in the Spring to deal with the second wave and some of them, including Sweden’s neighbors (except for ~250,000 people in Denmark who have been put in lockdown to prevent the mutated virus that emerged in mink farms from spreading), have decided to forego lockdowns entirely. On the other hand, Sweden has decided to tighten restrictions somewhat, but while they are now pretty similar to the restrictions in other Nordic countries, they are still far more relaxed than what most European countries are doing. It’s a testament to how much ideology colors perception that people now seem to be convinced that Sweden has decided to adopt the policies used in the rest of Europe, when it’s completely obvious to anyone who actually looks at the facts that other European countries have moved closer to the policies used by Sweden in the Spring than the other way around. However, in many cases, I think the restrictions they used are still more stringent than what is desirable from a cost-benefit perspective and certainly more stringent than what is necessary to push below 1. (Of course, I’m not saying that the optimal level of restriction is the same in every country, there is no reason to think that and it’s likely that more stringent restrictions are required in some countries than others.) But again this is a story for another time.

Conclusion

I have no doubt that lockdowns saved lives, but they didn’t save nearly as many as people think and they certainly didn’t save 3 million lives in Europe alone during the first wave, as Flaxman et al. claim. They use sophisticated statistical techniques to reach a conclusion that can be rejected with a high degree of certainty just by eyeballing a chart. Their paper is a prime example of propaganda masquerading as science that weaponizes complicated mathematics to promote questionable policies. Complicated mathematics always impresses people because they don’t understand it and it makes the analysis look scientific, but often it’s used to launder totally implausible assumptions, which anyone could recognize as such if they were stated in plain language. I think it’s exactly what happened with Flaxman et al.’s paper, which has been used as a cudgel to defend lockdowns, even though it has no practical relevance whatsoever. The truth is that, with the data and methods they used, it’s impossible to estimate the effect of non-pharmaceutical interventions and anyone who claims otherwise is selling snake oil.

To be clear, while I personally think it’s best to avoid lockdowns, I don’t claim to have demonstrated that. I only claim that, even if you think that lockdowns are the way to go, you shouldn’t use Flaxman et al.’s paper to argue for that view, because it has no practical relevance whatsoever. People sometimes ask why I joke that I’m anti-science, but this is why. Scientific journals, even very prestigious ones, routinely publish this kind of papers that claim to have policy relevance but don’t actually have any. It’s essentially voodoo magic for the “I love science” crowd, where the colorful rituals have been replaced by scary-looking mathematical formulas. This is especially likely to happen when, as in the case of the pandemic, the topic is politicized. As they say about sausages, once you know how they’re made, you often no longer want to eat them. Well, with science, it’s the same thing.

Finally, a lot of people have criticized preprints and stressed the importance of peer review during the pandemic, but note that the problem here isn’t the lack of peer review. Flaxman et al.’s paper was peer reviewed and published at one of the most prestigious scientific journals in the world, but it’s still garbage. In fact, not only was the problem not the lack of peer review, but I think this episode illustrates some of the problems with pre-publication peer review. Although I can’t prove it, it’s very likely that Flaxman et al. decided to hide the country-specific effect for Sweden because they knew that it would make it more difficult for them to publish their paper in Nature and scientists have very strong incentives to publish in prestigious journals, which would not exist if we abolished pre-publication peer review and journals as they currently exist. Moreover, precisely because it was peer reviewed and published in a prestigious journal, this paper was able to play a huge role in the policy debate. If pre-publication peer review didn’t exist, on the other hand, it would just have been another paper without the credibility granted to it by peer review and the affiliation with a prestigious journal, which always impress people who can’t judge the quality of a scientific paper and even many who can.

ADDENDUM: Some people seem to think that I’m a bit harsh on Flaxman et al. when I say that sweeping under the rug Sweden’s huge country-specific effect comes very close to scientific malpractice. One suggestion I have read is that perhaps they didn’t notice that the country-specific effect was so huge for Sweden, but I don’t buy that for a second. First, as I noted above, it’s pretty obvious from the results they describe in the paper that Sweden’s country-specific effect must be gigantic. There were 15 co-authors on this paper, so if I noticed it even though I have no formal training in epidemiology, I don’t see how it’s possible that none of them did. But perhaps more importantly, they published this figure in the supplementary materials, which shows the combined effect of the global and country-specific effects of lockdown for each country: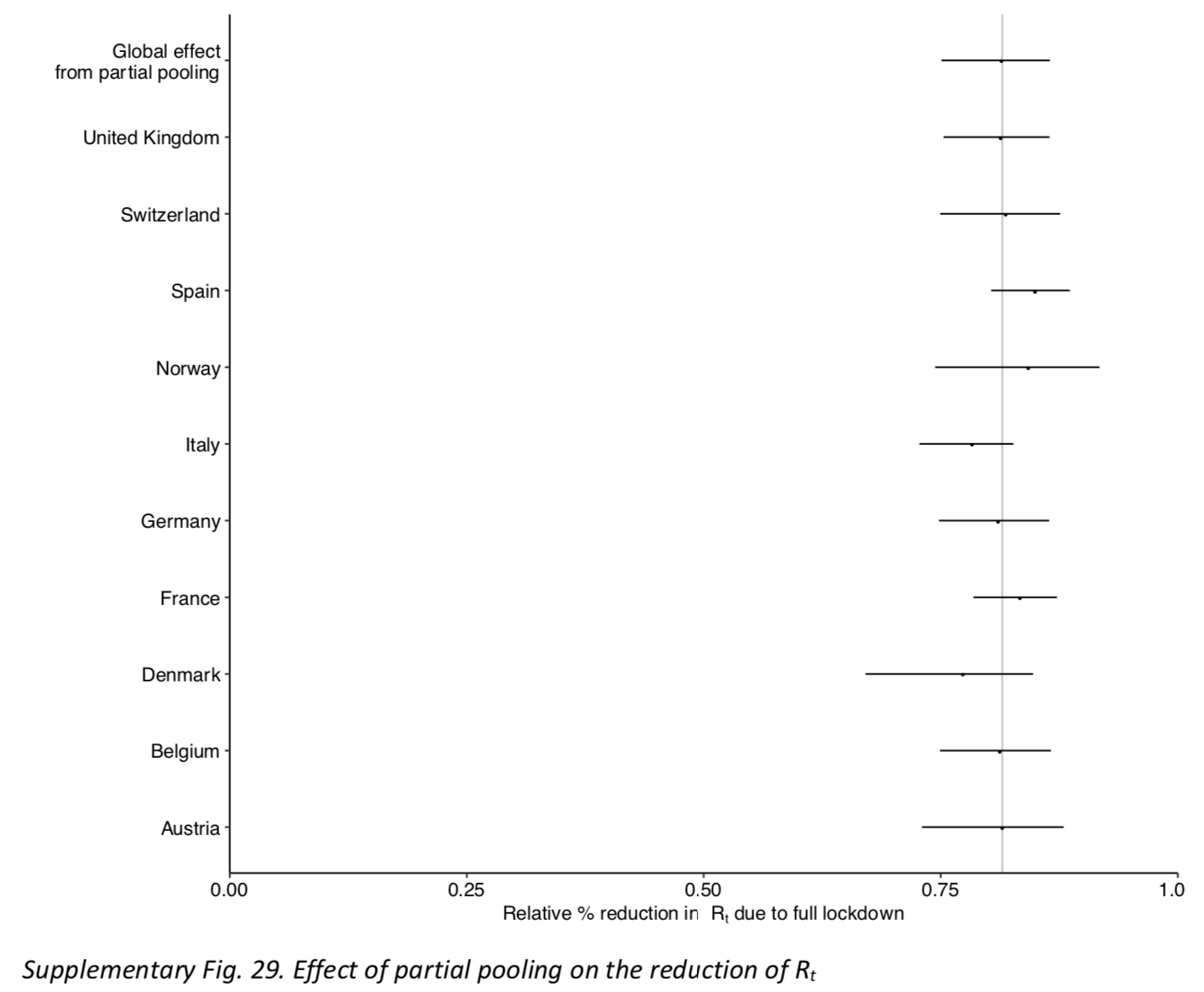So I know that they looked at the country-specific effects, because they had to in order to make this figure. Moreover, this figure conveniently omits Sweden and, by combining the global effect of lockdown with the country-specific effect, it hides the fact that the credible intervals on the country-specific effect are extremely wide. You could say that, since this chart is only about the impact of pooling on the effect of lockdowns, it made sense to exclude Sweden, but it doesn’t actually make sense to exclude Sweden if you want to assess the impact of pooling, even if the last intervention in Sweden wasn’t a lockdown. In any case, if they looked at the country-specific effects to make this figure (which again they had to), it beggars belief that they didn’t also look at the effect in Sweden, especially given that it’s the only way to make sense of the results they present in the paper. So of course they knew about this problem, they just swept it under the rug because they knew it was undermining their conclusion, without which their paper would probably not have been published in Nature. If they told me that they didn’t know about it, I simply wouldn’t believe them and neither should you. There is a difference between charity and stupidity.

EDIT: I fixed the table that showed the number of lives saved when you use the alternative counterfactual with the non-pooled model, because there was a mistake in the row about Sweden. (In this counterfactual, is reduced in every country on the day it started a lockdown by the overall effect of interventions in Sweden, but is unaffected before that. I had forgotten to make sure that, in the case of Sweden, interventions before the last affect . Thus, the table was saying that several thousands deaths would have been averted in Sweden if the country had used the policy it actually used, which didn’t make sense. The rest of the table was unaffected except perhaps for a few minor differences due to the fact that I ran the sampling algorithm for more iterations to explore the posterior distribution more thoroughly.) Obviously, the number of deaths averted once you fix the mistake is actually somewhat lower, so it doesn’t make any difference to my argument. While I was at it, I uploaded all the figures for every country and every model on GitHub, so people can have a look at the figures I didn’t show in the post without having to run the code, which is very computationally intensive and takes more than a day to run on my laptop.