A couple of days ago Mansa Keita, a computer scientist, tweeted about a 16-year-old black prodigy who lives in the UK:
A quick Google search reveals this story had first been reported in 2014, back when Ramarni — Wilfred is apparently his last name — was only 11, but he was back in the news earlier this year for some reason, even though the story was exactly the same.
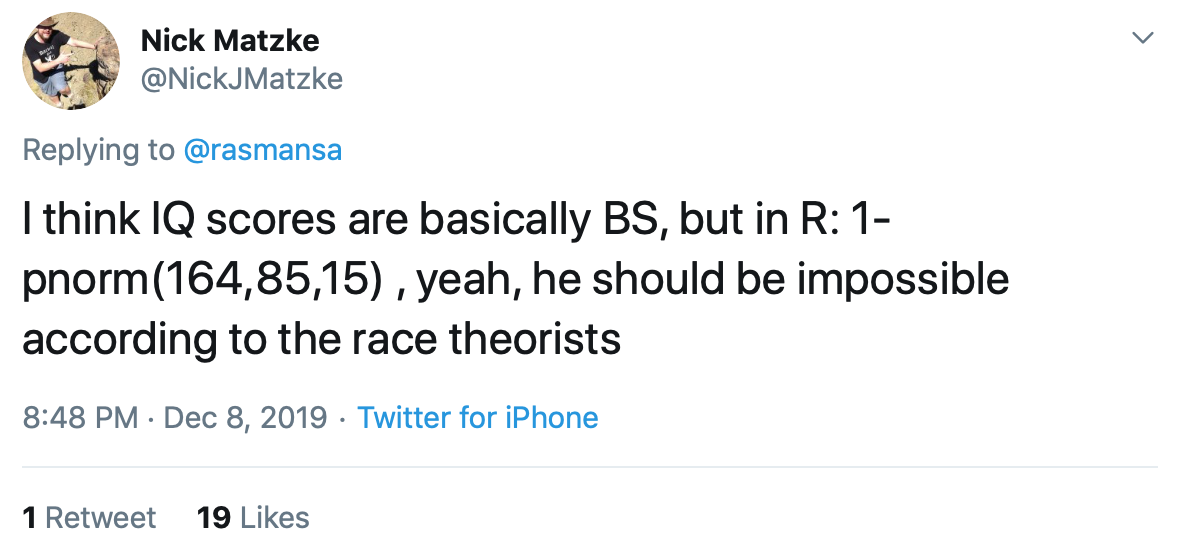
I don’t think Einstein and Hawking ever took an IQ test, so presumably the part of the story that says Ramarni scored higher than them is journalistic nonsense, but in any case 162 is a very high IQ. Indeed, it’s so high that several people reacted to Keita’s tweet by saying that, if “race theorists” were correct, Ramarni should not exist:
I’m not sure who the “race theorists” Matzke, who is apparently a biologist, is referring to, but judging from the discussion on Twitter I think he is talking about hereditarians who believe that the black/white IQ gap is partly genetic.
If I’m right, not only is this not true, but I also don’t think it has any bearing on the debate between hereditarians and environmentalists. First, if we assume that among black people IQ is normally distributed with a mean of 85 with a standard deviation of 15, which is what Matzke is doing above, then we should expect about 1.42 in 10 million black people to have an IQ greater than or equal to 162. Obviously, that is a very small probability, but it’s not zero. Moreover, I think the assumptions underlying this calculation, mean IQ of 85 and standard deviation of 15, are based on African-Americans, but my understanding is that black people in the UK are predominantly immigrants positively selected on education and their descendants, so they probably have a higher mean IQ. But even if we assume a mean IQ of 85, the probability is not zero, so I don’t understand why people say that, on those assumptions about the distribution of IQ among black people in the UK, Ramarni should be a statistical impossibility.
Back in 2011, there were about 1.9 million black people in the UK, which given the rate at which this group is growing — black people’s share of the population doubled between 2001 and 2011 — probably means there are more than 2.5 million of them today. Therefore, the expected number of black people in the UK with an IQ greater than or equal to 162 is about 0.35, which is less than 1. This may be why people say that Ramarni is a statistical impossibility, but if that’s why then it obviously doesn’t follow, for the same reason that, even though the expected value of a single roll of a fair six-sided dice is 3.5, it doesn’t mean that you can never land a 6 on your first try. So, even if we assume that Ramarni has an IQ of 162 and that black people in the UK have an IQ that is normally distributed with a mean of 85 and a standard deviation of 15, it doesn’t follow that he is a statistical impossibility. I’m sure he will be glad to learn that, but since he clearly is ridiculously smart, he probably had already figured it out.
In fact, this back-of-the-envelope calculation probably underestimates the expected number of black people in the UK with an IQ greater than or equal to 162, so it makes Ramarni’s existence more unlikely than it actually is. I already noted that, perhaps because in the UK blacks are positively selected on education, the mean of their IQ distribution is probably higher than 85, so the probability that a randomly selected black person in the UK has an IQ greater than or equal to 162 is likely greater than 1.42 in 10 million and the expected number of black people in the UK with an IQ that high is probably greater than 0.35. But in addition to that, because we have to take into account measurement error, it’s unlikely that Ramarni really has an IQ of 162.
Even if he was administered a state-of-the-art IQ test in ideal conditions, which we don’t know, no test is ever free of measurement error. Whenever someone scores absurdly high on a test, it’s likely that part of it was due to chance, so that his true score is lower. Similarly, when someone scores absurdly low on a test, it’s likely that it was partly due to chance, so that his true score is higher. Even if nobody can score more than 4 standard deviations above the mean on an IQ test without being extremely smart, when someone gets that kind of score, it’s probably in part because there was just the right alignment of planets on that day and they wouldn’t score as high if they took the test again. This is similar to how, in order to break a world record, even a superior athlete has to benefit from extremely favorable conditions. Even the person who holds a world record is not capable of achieving that kind of performance routinely. Thus, although there can be no doubt that Ramarni’s true IQ is extremely high, it’s probably somewhat lower than 162.
In order to estimate how much lower, we can use Bayesian statistics. On this approach, a person’s true IQ is seen as a random variable, which is assumed at the outset to follow a certain distribution. As we get data that bears on this individual’s true IQ, we revise this prior distribution in a way that reflects this information. Specifically, the idea is that, before someone has even taken an IQ test, we know the distribution of IQ in the population. This should give us a sense of what to expect when that person takes a test, even if we don’t know anything about him, so we can use the distribution of IQ in the population as the prior distribution for that individual’s true IQ. (Of course, if we know that he belongs to a particular subpopulation and you know the distribution of IQ in that subpopulation, we should use that as prior rather than the distribution of IQ in the whole population.) Once the person in question has taken a test, we have data that bears specifically on him, so we can use the result to update the prior, which yields the posterior distribution of his true IQ.
Let’s assume that, in the population to which the individual belongs, IQ follows the distribution
, where
is the mean and
is the standard deviation. IQ tests are actually designed to ensure this will be true. (Although I don’t think the procedure used can guarantee this assumption will hold at the tails, because presumably the test makers didn’t have a sample of millions of people to calibrate the test, but I don’t know enough about psychometrics to say how much reality departs from the normal model.) Furthermore, let’s assume that, when
takes an IQ test, his score can be modeled by a random variable
, where
is the true IQ of
and
is the standard error of measurement. From what I understand, as a matter of empirical fact, this is approximately true. On those assumptions, the posterior distribution of
is also normally distributed.
After has taken an IQ test, and has obtained the score
, we want to know the value of
, i. e. the mean of the posterior distribution of that individual’s true IQ. This is given by the formula
.
If you want to know how to derive it, you can read section 3.4 of this paper, which is actually chapter 3 of this book. (It also contains a derivation of the formula for the standard deviation, in case you’re interested.) As you can see, the mean of the posterior distribution is a weighted average of the mean of the population and the individual’s observed IQ, where the weights are respectively the square of the standard error of measurement and the square of the standard deviation of IQ in the population divided by the same constant in both cases.
Now, unless the IQ test that took is very unreliable, the standard error of measurement is much smaller than the the standard deviation of IQ in the population. (Moreover, the difference grows quickly when they are squared, as they are in the formula for the mean of the posterior distribution.) That’s because among people who scored the same as
on the test, true IQ scores presumably don’t spread much (otherwise the IQ test wouldn’t be very useful since the whole point is to be able to discriminate between people), whereas in the population as a whole there is a lot of variation. Hence, the mean of the posterior distribution will mostly depend on the score
obtained when it took the test, which makes perfect sense. But as the formula shows, it will not only depend on that, the mean of the population will also affect it somewhat.
The reason is that, even though people tend to think that, once you know the score a person got on the test, knowing how IQ is distributed in the population won’t help you better estimate that person’s IQ, this is actually wrong. Even when you know what score got on the test, knowledge about how IQ is distributed in the population is still informative about his true IQ, because it tells you something about how measurement error is likely to have affected his observed IQ. (This is a point I have already made a bit differently in my post about affirmative action, which you may also want to read.) Of course, it’s not nearly as informative as the score
obtained on the test, but it’s still a little bit informative. If I tell you that a kid in a special education class scored 150 on an IQ test, you will find that much harder to believe than if I tell you the kid was in a class for gifted students.
Now let’s go back to Ramarni. Based on the news reports I found, when he was tested at age 11, he scored 162. Apparently, for the Wechsler Intelligence Scale for Children (a high-quality IQ test for children between the ages of 6 and 16), the standard error of measurement is slightly greater than 3 at this age. We assumed that, in the UK, blacks have a mean IQ of 85 and a standard deviation of 15. (However, as I noted above, this is probably false. The mean is most likely higher and, although I have never seen data bearing on that, selection on education among black immigrants could also result in a lower standard deviation.) Therefore, if we apply the formula above, we conclude that, although Ramarni scored 162, his true IQ is probably a bit shy of 159. (If we assume that the standard error of measurement was 5 instead of 3, because the test he took was not as reliable as WISC-IV and/or because it wasn’t administered in ideal conditions, our estimate of his true IQ would be approximately 154.) If Ramarni had been white, since the mean of IQ is higher among whites, our estimate of his true IQ would have been a little bit higher (159.4 instead of 158.8), but not by much.
Clearly, it doesn’t change the fact that he is ridiculously smart, but this difference of 3 points still matters because, when you’re so far away from the mean and the variable of interest is distributed normally, the probability falls very quickly. Indeed, instead of 1.42 in 10 million, the probability that a randomly selected black person in the UK has an IQ greater than or equal to our best estimate of Ramarni’s true score is approximately 4.25 in 10 million. Thus, if we still assume that in 2019 there are about 2.5 million black people in the UK, the expected number of black people with an IQ at least as high as our best estimate of Ramarni’s true score is now slightly above 1 instead of 0.35. If we assume that, because of selection or for whatever other reason (perhaps environmental factors that depress IQ for blacks in the US are less present in the UK), blacks in the UK have a mean IQ of 90 instead of 85, the probability is about 20 in 10 million and the expected number of black people above that threshold is approximately 5.2.
So it’s not true that, if the mean of IQ for blacks were really one standard deviation lower than for whites, Ramarni would be a statistical impossibility. Clearly, we wouldn’t expect many people like him, but we’d still expect a few. (Of course, no matter what assumptions you make about the distribution of IQ among blacks, he is clearly exceptional.) But what I find really weird is that some people on Twitter seem to think that Ramarni’s existence bears on the debate between hereditarians and environmentalists about the causes of the black/white IQ gap. I don’t claim to be a specialist of this debate, but as far as I can tell, the existence and, to a large extent, the magnitude of this gap is not really in dispute. What environmentalists and hereditarians disagree about is the causes of that gap. Environmentalists are called like that because they think the causes are purely environmental and that genetics plays no role. If they didn’t think there was a gap, there would be nothing for environmental factors to explain. Personally, I think that, in many contexts where people bring up between-group differences in IQ, it doesn’t actually matter what causes them, but that’s a discussion for another post.